Hi, there. I'm happy to help with this.
 Prompt
Prompt:
The area of a rectangular lot is 900 feet. What is the length of the lot?So, if it has length L and width W, then L*W = 900. So far, we have one equation with two unknowns.
Statement #1:
The length of the lot is 25 feet greater than the width.In other words, L = 25 + W. Now we have two equations with two unknowns. That's a situation in which we are able to solve for definitive values of the variables. As it happens, L = 45, W = 20. Statement #1, by itself, is
sufficient.
Statement #2:
If the lot were separated into three unequal sections with two of the sections being square, the remaining section would have a length of 5 feet.What's not clear about this statement is: are all three of the sections unequal, which means the squares have to be different sizes, or it is just saying that not all three of sections are the same dimensions?
If the squares can be the same size, then one solution is possibility #1:
Attachment:
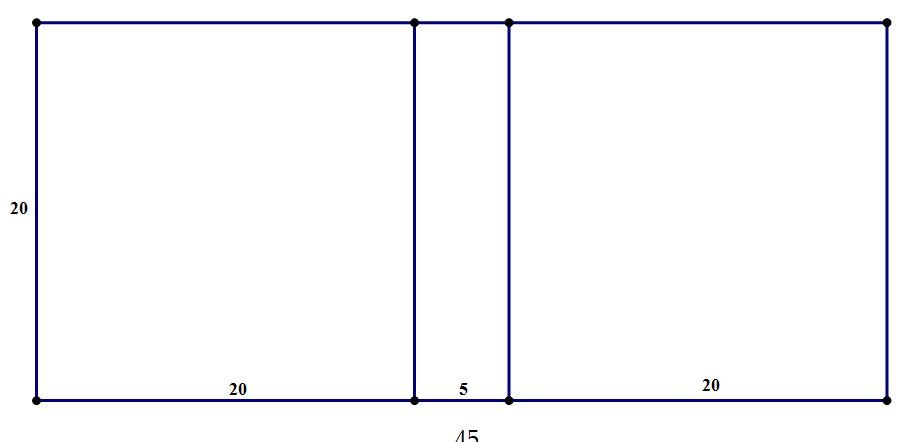 section possibility #1.JPG [ 28.05 KiB | Viewed 3584 times ]
section possibility #1.JPG [ 28.05 KiB | Viewed 3584 times ]
If the squares are not equal, we get a set up like this:
Attachment:
 section possibility #2.JPG [ 22.71 KiB | Viewed 3603 times ]
section possibility #2.JPG [ 22.71 KiB | Viewed 3603 times ]
Equating the left and right sides of this figure, we get L - W + 5 = W. That's a second equation relating L and W. As it happens, this gives solutions of L = 40, W = 22.5. Thus, statement #2 produces more than one possibility, so it is
insufficient.
Does all this make sense? Please let me know if you have any further question on this.
Mike


 65%
(hard)
65%
(hard)
 42%
(02:16)
wrong
42%
(02:16)
wrong  based on 198
sessions
based on 198
sessions