If |x - 3| - |x - 4| = |x - 6|, what is the value of x?

Provided the question has been transcribed correctly, it could not appear on the GMAT™ as such. The GMAT™ will always provide consistent information about an unknown between the two statements. Since Statement (1) looks like an easier entry point, how about we start there?

Statement (1)

\(x^2 = 25\)

\(|x| = 5\)

x = 5 or -5

Only one of these solutions is valid.

\(|(5) - 3| - |(5) - 4| = |(5) - 6|\)

\(|2| - |1| = |-1|\)

\(2 - 1 = 1\) √

\(|(-5) - 3| - |(-5) - 4| = |(-5) - 6|\)

\(|-8| - |-9| = |-11|\)

\(8 - 9 = 11\) X

So, Statement (1) is SUFFICIENT, since x can only equal 5. But when we look at Statement (2), we can see pretty quickly that x will not be equal to 5:

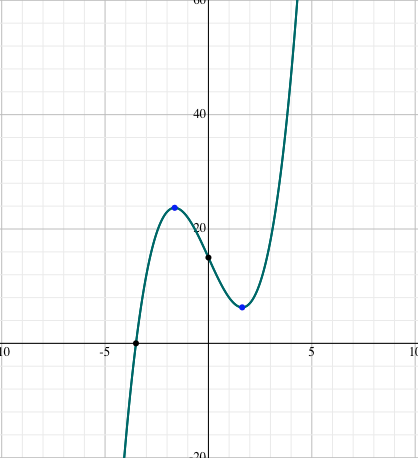
\(x^3 - 8x + 15 = 0\)

\((5)^3 - 8(5) + 15 = 0\)

\(125 - 40 + 15 = 0\)

\(100 = 0\) X

The point of a well written DS question is to provide consistent information between statements, to see if they reveal enough overlapping information to answer the question on their own. It cannot be true that x can equal 5 in one case and not 5 in another. The other statement might not allow us to figure out that x = 5, but we should never see conflicting information. The graph of the polynomial in Statement (2) shows that the solution is around -3.5.

As I said before, either this question was not transcribed correctly, or it is not a GMAT™-like DS question.

- Andrew