Forum Home > GMAT > Quantitative > Problem Solving (PS)
Events & Promotions
|
|
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Dec 1511:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease.
Dec 1608:00 AM PST
-11:59 PM PST
GMAT Club 12 Days of Christmas is a 4th Annual GMAT Club Winter Competition based on solving questions. This is the Winter GMAT competition on GMAT Club with an amazing opportunity to win over $40,000 worth of prizes!- Dec 17
09:00 AM PST
-10:00 AM PST
Join Manhattan Prep instructor Whitney Garner for a fun—and thorough—review of logic-based (non-math) problems, with a particular emphasis on Data Sufficiency and Two-Parts. - Dec 18
10:00 AM PST
-11:00 AM PST
Here is the essential guide to securing scholarships as an MBA student! In this video, we explore the various types of scholarships available, including need-based and merit-based options.
Updated on: 13 Feb 2019, 19:34
Originally posted by ChiranjeevSingh on 09 Feb 2019, 06:38.
Last edited by ChiranjeevSingh on 13 Feb 2019, 19:34, edited 1 time in total.
Last edited by ChiranjeevSingh on 13 Feb 2019, 19:34, edited 1 time in total.
Kudos
Bookmarks
I am thoroughly excited to present this article. This article is a result of my analysis of 75 ESRs I’ve gotten from students, mine or otherwise. From the analysis, I’ve tried to answer some of the most frequently asked questions by GMAT aspirants such as:
1. Do Verbal and Quant Scores have equal weights in the Total Score?
2. In Verbal, is there any one sub-section (CR, SC, or RC) significantly more important than the other two?
3. How many questions can I get wrong to reach a certain Verbal or Quant score?
4. What is the maximum Verbal or Quant score can I reach if I get a certain number of questions wrong?
5. Why is it so much easier to score a Q45 than a V45? Why has GMAC made it much more difficult to score high on Verbal than on Quant?
6. Are the first few questions more important than the remaining ones?
7. Does the GMAT algorithm follow a fixed pattern i.e. giving similar difficulty level of questions for similar performance?
Are you excited to know, probably for the first time, data-driven answers to the above questions?
I definitely am.
Let’s get started.
Do Verbal and Quant Scores have equal weights in the Total Score?
The short answer is YES.
And at the end of this answer, I’m going to give you a formula with which you can calculate the total score of anybody by just knowing their quant and verbal scores, without looking up any calculator or chart online!
The reasoning behind the answer (i.e. YES) is two-fold (the two folds are inter-related to an extent):
1. The correlation between Total Score and the Sum of Verbal and Quant scores is almost 1 (0.994 to be precise). This means that Total Score is a linear function of the Sum of the two scores. Besides, when I try to assign ‘different’ weights to the Verbal and the Quant scores, the correlation between the Total Score and Weighted Sum turns out to be lower, indicating that the actual weight is equal to 1.
2. I can very accurately predict the total scores of all the 75 items in my list by simply multiplying a constant with the Sum of the two scores (Verbal and Quant).
Correlation is a Statistics term that varies between -1 and 1. Higher the magnitude of correlation, stronger the relationship between variables. A correlation of +1 or -1 indicates perfect relationship, meaning that one can ‘accurately’ estimate the value of one variable using the value of the other variable. A positive correlation means that both variables change in the same direction i.e. both increase at the same time or decrease at the same. A negative correlation means that the variables change in opposite directions i.e. if one increases, the other decreases. A zero correlation means that the two variables are completely independent. An example of zero correlation could be the correlation between the number of hairs on a person’s body and his GMAT score.
Both the above observations indicate that a point in Verbal is equivalent to a point in Quant in terms of its impact on the total score.
One quite expected observation from the data is a very low correlation between Quant and Verbal scores (0.12 to be precise). Such a correlation indicates that the two sections are testing very different skills. While this is quite obvious, I found it interesting to verify this from the data.
Now, comes the formula for calculating the total score of a person from his/her Quant and Verbal scores.
Let’s denote the Quant score with Q and the Verbal score with V.
Total Score = 8.25*(Q+V)
i.e. you add up the Quant and Verbal scores of the person and multiply the sum with 8.25 to get his Total Score.
Now, the obvious question is: how accurate is the formula?
The answer is very accurate. Using this formula, I could calculate the Total Score exactly i.e. without error in 50% of the cases, within ±10 points in 90% of the cases, and within ±20 points in 100% of the cases i.e. my calculation ‘never’ overshot or undershot the actual score by more than 20 points. If you have been paying attention to the GMAT scores and Verbal-Quant splits of others, you’d already know that this much variation i.e. ±20 points is seen in Total scores with same Quant and Verbal splits. In this way, the above formula seems as precise as a derived formula can get.
You can try out this formula on your past GMAT scores or on the scores of your known ones. However, I understand that the formula doesn’t look very easy to calculate without a calculator. One way to skip the calculator is to recognize that 8.25 is equal to 33/4. So, you can arrive at the total score by dividing the sum of Quant and Verbal scores by 4 and then multiplying the result with 33.
If this way still appears difficult and you are ok with slight imprecision, you can arrive at the total score by dividing the sum of Quant and Verbal scores by 12 and then multiplying the result with 100. I hope this should not be very difficult. This result is slightly imprecise since we are multiplying 8.33 instead of 8.25. However, this formula gives you a good estimate without involving difficult calculations.
Total Score = ((Q + V)/12)*100
We can call this way of calculating the total score - CJ’s formula ? I don’t mind taking credits!
(This formula gives accurate results for a large range of Total Scores (400-770). For scores lying on the extremes (either <400 or >770), the formula may not yield as accurate results.)
In Verbal, is there any one sub-section (CR, SC, or RC) significantly more important than the other two?
The short answer is No.
However, let me put a disclaimer: the data doesn’t provide as clear an answer to this question as it did to the previous question.
Now, let me tell you how I went about to answer this question.
First of all, I tried to figure whether each of the three sub-sections is equally important. If the average of the three sub-sectional scores is always (or almost always) equal to the Verbal score, it will very strongly indicate that all three sections are equally important since the Verbal score is just an average of the three scores.
From the data, I see that the average of the three scores (individual CR, RC, and SC scores) is a very good estimate of the total score, with correlation equal to 0.98 and SD equal to 1.24. SD (square root of the average squared difference) of 1.24 means that on an average, you can expect a difference of 1.24 between the actual Verbal score and the average of the three sectional scores. I found this number neither too low to ignore the average of three sub-sectional scores as a good estimate for the Verbal score nor too high to consider the average to be an ‘excellent’ estimate for the Verbal score.
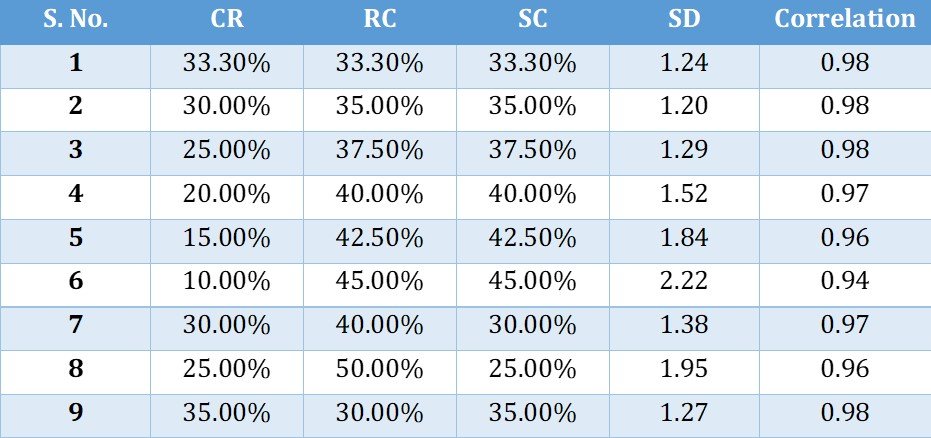
Thus, the data didn’t provide a convincing answer to this question. However, then, I tried assigning different weights to the three sections to see whether these two parameters (correlation and SD) – become favorable for a particular set of weights - favorable means high correlation and low SD. I found the following data.
ESR 1.jpg [ 104.36 KiB | Viewed 6319 times ]
What I could observe was that for smaller changes in the comparative weights of the three sections (i.e. in cases 1,2,3, and 9), the SD and Correlation numbers were so close that I could not choose one set of weights over the others. The differences could be entirely due to randomness in the data.
However, I could also see that as I started bringing in bigger changes in the comparative weights of the three sections (i.e. 4, 5, 6, and 8), both SD and Correlation numbers started turning rapidly in the adverse direction, indicating that there are no significant differences in the weights or importance of these three sub-sections.
From my data, while I cannot rule out slight differences in the weights of the three sub-sections, I don’t think there are significant differences in the weights.
On a side note, I also found the correlations among the sub-sectional scores i.e. CR, RC, and SC.
Correlation between CR and RC: 0.326
Correlation between CR and SC: 0.146
Correlation between SC and RC: 0.316
A greater correlation means that the two scores have a greater propensity to move in tandem. An interesting observation is a very low correlation between CR and SC scores, indicating that the two scores are almost independent i.e. we cannot judge a person’s CR ability from his SC ability or vice-versa.
How many questions can I get wrong to reach a certain Verbal or Quant score?
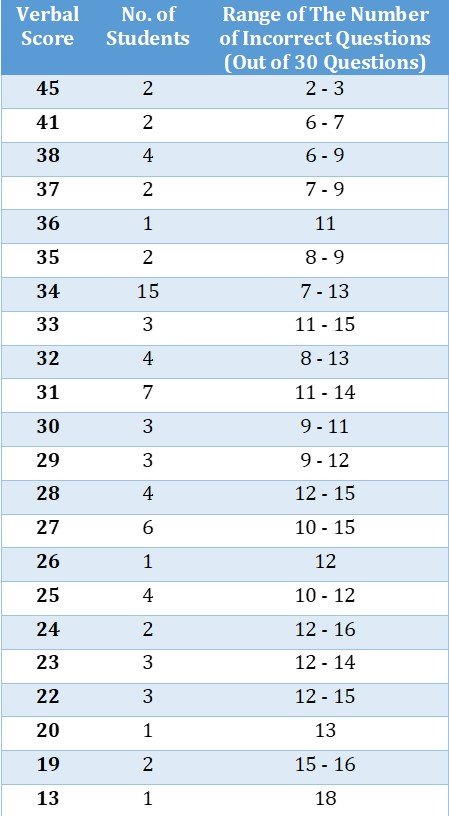
Here’s the table for Verbal:
ESR 2.jpg [ 71.96 KiB | Viewed 6344 times ]
The first column lists the Verbal score, the second column the number of students with that Verbal score, and the third column the range of the number of incorrect questions for that Verbal score. (Please note that ESRs contain data for only the scored questions (30 in Verbal and 28 in Quant) and not the experimental questions. Thus, the numbers of incorrect questions in the above table are out of 30.)
For example:
In my data of 75 ESRs, 15 ESRs had a Verbal Score of 34. The maximum number of questions a person with a V34 got incorrect was 13, and the corresponding minimum number was 7. Thus, if you are targeting a V34, you can get 7-13 questions wrong.
We can see that there is a good amount of overlap in the ranges for different scores. Getting 13 questions wrong can land you at V34 or even at V20!! (The guy with V20 in my data also got 13 questions wrong, as can be seen from the table above)
Given such a good amount of overlap of the number of incorrect questions across different scores, we can see something most of us already know that it’s not just about the number of questions you get right or wrong; it’s also about the difficulty level of the questions you get right or wrong.
Here’s the table for Quant.
ESR 3.jpg [ 53.68 KiB | Viewed 6354 times ]
The interesting observation from the above data is that there is no overlap between Q50 and Q49 in terms of the number of incorrect questions. This means that if you get 4 questions wrong, you’ll get a Q50 and if you get one more question wrong, you land up at Q49. (Even though these ranges may change once we get data from more ESRs, I find this data reliable to a large extent since there are 6 data points for Q50 and 20 data points for Q49.)
This post was originally posted on this link: https://gmatwithcj.com/articles/data-dri ... at-part-1/
You can find the second part of this article on this link: https://gmatwithcj.com/articles/data-dri ... at-part-2/
You can find the third part of this article on this link: https://gmatwithcj.com/articles/data-dri ... at-part-3/
1. Do Verbal and Quant Scores have equal weights in the Total Score?
2. In Verbal, is there any one sub-section (CR, SC, or RC) significantly more important than the other two?
3. How many questions can I get wrong to reach a certain Verbal or Quant score?
4. What is the maximum Verbal or Quant score can I reach if I get a certain number of questions wrong?
5. Why is it so much easier to score a Q45 than a V45? Why has GMAC made it much more difficult to score high on Verbal than on Quant?
6. Are the first few questions more important than the remaining ones?
7. Does the GMAT algorithm follow a fixed pattern i.e. giving similar difficulty level of questions for similar performance?
Are you excited to know, probably for the first time, data-driven answers to the above questions?
I definitely am.
Let’s get started.
Do Verbal and Quant Scores have equal weights in the Total Score?
The short answer is YES.
And at the end of this answer, I’m going to give you a formula with which you can calculate the total score of anybody by just knowing their quant and verbal scores, without looking up any calculator or chart online!
The reasoning behind the answer (i.e. YES) is two-fold (the two folds are inter-related to an extent):
1. The correlation between Total Score and the Sum of Verbal and Quant scores is almost 1 (0.994 to be precise). This means that Total Score is a linear function of the Sum of the two scores. Besides, when I try to assign ‘different’ weights to the Verbal and the Quant scores, the correlation between the Total Score and Weighted Sum turns out to be lower, indicating that the actual weight is equal to 1.
2. I can very accurately predict the total scores of all the 75 items in my list by simply multiplying a constant with the Sum of the two scores (Verbal and Quant).
Correlation is a Statistics term that varies between -1 and 1. Higher the magnitude of correlation, stronger the relationship between variables. A correlation of +1 or -1 indicates perfect relationship, meaning that one can ‘accurately’ estimate the value of one variable using the value of the other variable. A positive correlation means that both variables change in the same direction i.e. both increase at the same time or decrease at the same. A negative correlation means that the variables change in opposite directions i.e. if one increases, the other decreases. A zero correlation means that the two variables are completely independent. An example of zero correlation could be the correlation between the number of hairs on a person’s body and his GMAT score.
Both the above observations indicate that a point in Verbal is equivalent to a point in Quant in terms of its impact on the total score.
One quite expected observation from the data is a very low correlation between Quant and Verbal scores (0.12 to be precise). Such a correlation indicates that the two sections are testing very different skills. While this is quite obvious, I found it interesting to verify this from the data.
Now, comes the formula for calculating the total score of a person from his/her Quant and Verbal scores.
Let’s denote the Quant score with Q and the Verbal score with V.
Total Score = 8.25*(Q+V)
i.e. you add up the Quant and Verbal scores of the person and multiply the sum with 8.25 to get his Total Score.
Now, the obvious question is: how accurate is the formula?
The answer is very accurate. Using this formula, I could calculate the Total Score exactly i.e. without error in 50% of the cases, within ±10 points in 90% of the cases, and within ±20 points in 100% of the cases i.e. my calculation ‘never’ overshot or undershot the actual score by more than 20 points. If you have been paying attention to the GMAT scores and Verbal-Quant splits of others, you’d already know that this much variation i.e. ±20 points is seen in Total scores with same Quant and Verbal splits. In this way, the above formula seems as precise as a derived formula can get.
You can try out this formula on your past GMAT scores or on the scores of your known ones. However, I understand that the formula doesn’t look very easy to calculate without a calculator. One way to skip the calculator is to recognize that 8.25 is equal to 33/4. So, you can arrive at the total score by dividing the sum of Quant and Verbal scores by 4 and then multiplying the result with 33.
If this way still appears difficult and you are ok with slight imprecision, you can arrive at the total score by dividing the sum of Quant and Verbal scores by 12 and then multiplying the result with 100. I hope this should not be very difficult. This result is slightly imprecise since we are multiplying 8.33 instead of 8.25. However, this formula gives you a good estimate without involving difficult calculations.
Total Score = ((Q + V)/12)*100
We can call this way of calculating the total score - CJ’s formula ? I don’t mind taking credits!
(This formula gives accurate results for a large range of Total Scores (400-770). For scores lying on the extremes (either <400 or >770), the formula may not yield as accurate results.)
In Verbal, is there any one sub-section (CR, SC, or RC) significantly more important than the other two?
The short answer is No.
However, let me put a disclaimer: the data doesn’t provide as clear an answer to this question as it did to the previous question.
Now, let me tell you how I went about to answer this question.
First of all, I tried to figure whether each of the three sub-sections is equally important. If the average of the three sub-sectional scores is always (or almost always) equal to the Verbal score, it will very strongly indicate that all three sections are equally important since the Verbal score is just an average of the three scores.
From the data, I see that the average of the three scores (individual CR, RC, and SC scores) is a very good estimate of the total score, with correlation equal to 0.98 and SD equal to 1.24. SD (square root of the average squared difference) of 1.24 means that on an average, you can expect a difference of 1.24 between the actual Verbal score and the average of the three sectional scores. I found this number neither too low to ignore the average of three sub-sectional scores as a good estimate for the Verbal score nor too high to consider the average to be an ‘excellent’ estimate for the Verbal score.
Thus, the data didn’t provide a convincing answer to this question. However, then, I tried assigning different weights to the three sections to see whether these two parameters (correlation and SD) – become favorable for a particular set of weights - favorable means high correlation and low SD. I found the following data.
Attachment:
ESR 1.jpg [ 104.36 KiB | Viewed 6319 times ]
What I could observe was that for smaller changes in the comparative weights of the three sections (i.e. in cases 1,2,3, and 9), the SD and Correlation numbers were so close that I could not choose one set of weights over the others. The differences could be entirely due to randomness in the data.
However, I could also see that as I started bringing in bigger changes in the comparative weights of the three sections (i.e. 4, 5, 6, and 8), both SD and Correlation numbers started turning rapidly in the adverse direction, indicating that there are no significant differences in the weights or importance of these three sub-sections.
From my data, while I cannot rule out slight differences in the weights of the three sub-sections, I don’t think there are significant differences in the weights.
On a side note, I also found the correlations among the sub-sectional scores i.e. CR, RC, and SC.
Correlation between CR and RC: 0.326
Correlation between CR and SC: 0.146
Correlation between SC and RC: 0.316
A greater correlation means that the two scores have a greater propensity to move in tandem. An interesting observation is a very low correlation between CR and SC scores, indicating that the two scores are almost independent i.e. we cannot judge a person’s CR ability from his SC ability or vice-versa.
How many questions can I get wrong to reach a certain Verbal or Quant score?
Here’s the table for Verbal:
Attachment:
ESR 2.jpg [ 71.96 KiB | Viewed 6344 times ]
The first column lists the Verbal score, the second column the number of students with that Verbal score, and the third column the range of the number of incorrect questions for that Verbal score. (Please note that ESRs contain data for only the scored questions (30 in Verbal and 28 in Quant) and not the experimental questions. Thus, the numbers of incorrect questions in the above table are out of 30.)
For example:
In my data of 75 ESRs, 15 ESRs had a Verbal Score of 34. The maximum number of questions a person with a V34 got incorrect was 13, and the corresponding minimum number was 7. Thus, if you are targeting a V34, you can get 7-13 questions wrong.
We can see that there is a good amount of overlap in the ranges for different scores. Getting 13 questions wrong can land you at V34 or even at V20!! (The guy with V20 in my data also got 13 questions wrong, as can be seen from the table above)
Given such a good amount of overlap of the number of incorrect questions across different scores, we can see something most of us already know that it’s not just about the number of questions you get right or wrong; it’s also about the difficulty level of the questions you get right or wrong.
Here’s the table for Quant.
Attachment:
ESR 3.jpg [ 53.68 KiB | Viewed 6354 times ]
The interesting observation from the above data is that there is no overlap between Q50 and Q49 in terms of the number of incorrect questions. This means that if you get 4 questions wrong, you’ll get a Q50 and if you get one more question wrong, you land up at Q49. (Even though these ranges may change once we get data from more ESRs, I find this data reliable to a large extent since there are 6 data points for Q50 and 20 data points for Q49.)
This post was originally posted on this link: https://gmatwithcj.com/articles/data-dri ... at-part-1/
You can find the second part of this article on this link: https://gmatwithcj.com/articles/data-dri ... at-part-2/
You can find the third part of this article on this link: https://gmatwithcj.com/articles/data-dri ... at-part-3/
Updated on: 13 Feb 2019, 19:36
Originally posted by ChiranjeevSingh on 10 Feb 2019, 06:50.
Last edited by ChiranjeevSingh on 13 Feb 2019, 19:36, edited 2 times in total.
Last edited by ChiranjeevSingh on 13 Feb 2019, 19:36, edited 2 times in total.
Kudos
Bookmarks
What is the maximum Verbal or Quant score can I reach if I get a certain number of questions wrong?
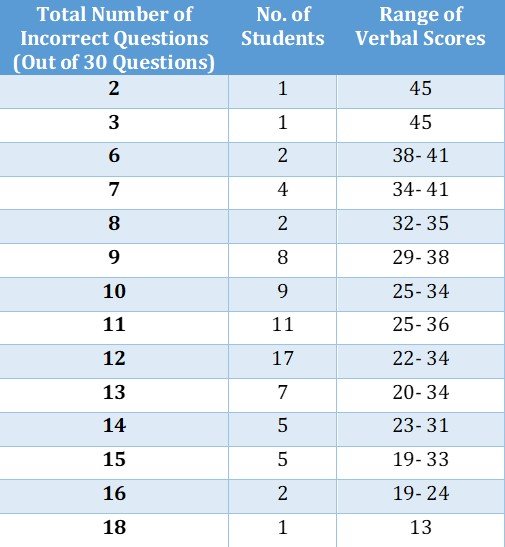
Here’s the data for Verbal:
ESR Verbal 2.jpg [ 53.59 KiB | Viewed 6244 times ]
As you can see, I don’t have a lot of data points (no. of students) for the smallest (2-6 incorrect questions) and the largest (>15 incorrect questions) number of incorrect questions entries. However, I have a decent number of data points for the entries in-between. One thing very clearly comes out is that for the same number of incorrect questions, you can get widely different scores. For example, with 12 questions wrong, you can get the lowest of V22 (i.e. 30 %ile) and the highest of V34 (i.e. 71 %ile), a very significant difference indeed.
Besides, it is also possible that a person with 15 questions wrong ends up getting a higher score than a person with just 8 questions wrong. There was indeed one such case in my data in which a person with 15 questions wrong had a V33 and a person with 8 questions wrong had a V32. You may be wondering how this is possible. How could a person get almost half the number of questions wrong compared to another person and still end up at a lower score? Did the person with V32 get a lot of initial questions wrong? We’ll look at these questions in the later sections of this article.
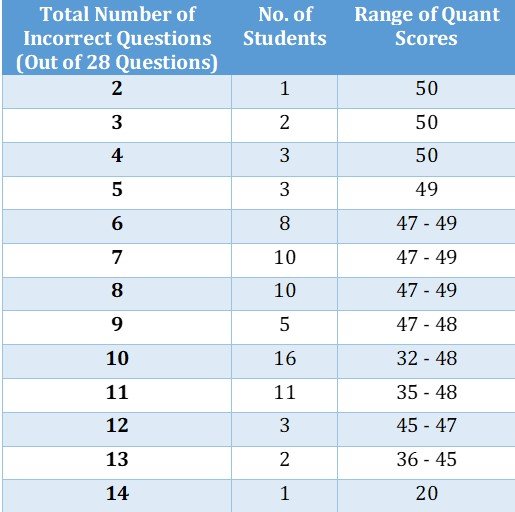
Here’s the data for Quant:
ESR Quant 2.jpg [ 50.84 KiB | Viewed 6232 times ]
We can observe in the above data that three students scored a Q50 with 4 questions wrong and three students who scored 5 questions wrong got a Q49 each. There seems to be some consistency at this end of the table. However, as we go down the table (6-13 questions wrong), we see that there are wide ranges of scores for different number of incorrect questions. For example, one student had a Q32 after getting 10 questions wrong and another who got 10 questions wrong had a Q48, a sea difference in the scores without any difference in the number of questions marked incorrect.
Clearly, the GMAT algorithm is driven a lot by the kind of question a person gets wrong. Logically, a person marking an easy question wrong should be punished more severely than a person getting a difficult question wrong. By getting an easy question wrong, a person is indicating that he cannot be depended on even for correctly solving simpler problems consistently. If you cannot depend on a person for consistently solving easier problems correctly, logically he deserves a low score. On the other hand, on difficult problems in life, a lot of us falter in some way or the other. So, getting a difficult question wrong shouldn’t be as significant a problem as getting an easier question wrong should be.
If you compare the Quant and Verbal tables above, you’ll see that while it is possible to get a Q45 with 13 questions wrong, in Verbal, the highest you get with 13 questions wrong is V34. It is quite clear that getting a V45 is nowhere as easy as getting a Q45. This brings us to our next question.
Why has GMAC made it much more difficult to score high on Verbal than on Quant?
At least a part of the answer seems to lie in their (the GMAC guys’) perception of the difficulty of the questions. Quant questions that are quite easy for an average Indian test taker are considered by GMAC more difficult than Verbal questions that are quite difficult for an average Indian test taker. In other words, a quant question of Medium difficulty level per GMAC is generally an easy question for an Indian test taker, whereas a Verbal question of Medium difficulty level per GMAC is generally a hard question for an Indian test taker.
How do I know this?
From the ESR reports.
What would be the level of difficulty of Quant questions a person who has scored a Q45 must have faced in the exam?
Most Indians would call such questions Easy-to-Medium.
GMAC doesn’t agree.
Here’s the difficulty level of the Quant questions that people who got Q45 faced:
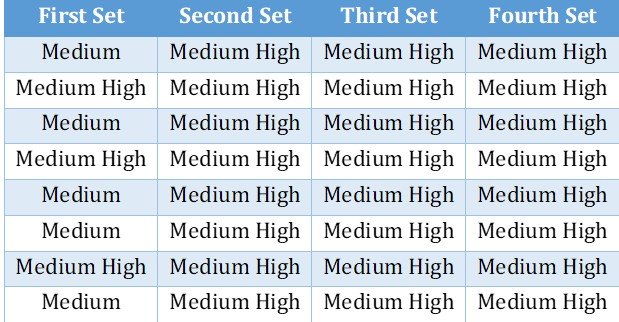
Quant Diff.jpg [ 85.81 KiB | Viewed 6214 times ]
As you can see, almost all the Quant questions that these people with Q45 faced were Medium-High. Now, let’s compare it with the level of difficulty of Verbal questions that people with V45 faced (I had only two such data points with me).
Verbal Diff.jpg [ 22.42 KiB | Viewed 6205 times ]
Per GMAC, the guys with V45 faced mainly medium-level Verbal questions, and medium-high questions only in the second quarter.
According to you, what would be the difficulty level of the Verbal questions a person with V45 would face?
Would you call that difficulty level ‘medium’?
I believe most of us, non-native speakers, will say no. At V45 level, we’d expect very difficult questions.
However, that is our perception, not GMAC’s perception.
Thus, even if you solve a lot of these questions correctly, you deserve a V45, not V51.
I think it’s easier to understand why there is such a difference in the perceptions of the difficulty level of questions. Indians are generally good at Quant and weak in Verbal. On the other hand, Americans are quite the opposite. Thus, GMAT, a test conducted by a US-based organization, is expected to reflect the perceptions it currently reflects.
To answer the question, GMAC hasn’t deliberately made it difficult to score high on Verbal than on Quant. We feel that GMAC has done so because with Verbal, our comfort is much less than the comfort of an average test-taker in America, in which GMAC is based. The Verbal questions that are pretty hard for us are manageable for them, and the quant questions that are manageable for us are pretty hard for them.
That’s it for this article. In the next article, we’ll answer the following questions:
You can find the next and last part of this article series on this link: https://gmatwithcj.com/articles/data-dri ... at-part-3/
Here’s the data for Verbal:
Attachment:
ESR Verbal 2.jpg [ 53.59 KiB | Viewed 6244 times ]
As you can see, I don’t have a lot of data points (no. of students) for the smallest (2-6 incorrect questions) and the largest (>15 incorrect questions) number of incorrect questions entries. However, I have a decent number of data points for the entries in-between. One thing very clearly comes out is that for the same number of incorrect questions, you can get widely different scores. For example, with 12 questions wrong, you can get the lowest of V22 (i.e. 30 %ile) and the highest of V34 (i.e. 71 %ile), a very significant difference indeed.
Besides, it is also possible that a person with 15 questions wrong ends up getting a higher score than a person with just 8 questions wrong. There was indeed one such case in my data in which a person with 15 questions wrong had a V33 and a person with 8 questions wrong had a V32. You may be wondering how this is possible. How could a person get almost half the number of questions wrong compared to another person and still end up at a lower score? Did the person with V32 get a lot of initial questions wrong? We’ll look at these questions in the later sections of this article.
Here’s the data for Quant:
Attachment:
ESR Quant 2.jpg [ 50.84 KiB | Viewed 6232 times ]
We can observe in the above data that three students scored a Q50 with 4 questions wrong and three students who scored 5 questions wrong got a Q49 each. There seems to be some consistency at this end of the table. However, as we go down the table (6-13 questions wrong), we see that there are wide ranges of scores for different number of incorrect questions. For example, one student had a Q32 after getting 10 questions wrong and another who got 10 questions wrong had a Q48, a sea difference in the scores without any difference in the number of questions marked incorrect.
Clearly, the GMAT algorithm is driven a lot by the kind of question a person gets wrong. Logically, a person marking an easy question wrong should be punished more severely than a person getting a difficult question wrong. By getting an easy question wrong, a person is indicating that he cannot be depended on even for correctly solving simpler problems consistently. If you cannot depend on a person for consistently solving easier problems correctly, logically he deserves a low score. On the other hand, on difficult problems in life, a lot of us falter in some way or the other. So, getting a difficult question wrong shouldn’t be as significant a problem as getting an easier question wrong should be.
If you compare the Quant and Verbal tables above, you’ll see that while it is possible to get a Q45 with 13 questions wrong, in Verbal, the highest you get with 13 questions wrong is V34. It is quite clear that getting a V45 is nowhere as easy as getting a Q45. This brings us to our next question.
Why has GMAC made it much more difficult to score high on Verbal than on Quant?
At least a part of the answer seems to lie in their (the GMAC guys’) perception of the difficulty of the questions. Quant questions that are quite easy for an average Indian test taker are considered by GMAC more difficult than Verbal questions that are quite difficult for an average Indian test taker. In other words, a quant question of Medium difficulty level per GMAC is generally an easy question for an Indian test taker, whereas a Verbal question of Medium difficulty level per GMAC is generally a hard question for an Indian test taker.
How do I know this?
From the ESR reports.
What would be the level of difficulty of Quant questions a person who has scored a Q45 must have faced in the exam?
Most Indians would call such questions Easy-to-Medium.
GMAC doesn’t agree.
Here’s the difficulty level of the Quant questions that people who got Q45 faced:
Attachment:
Quant Diff.jpg [ 85.81 KiB | Viewed 6214 times ]
As you can see, almost all the Quant questions that these people with Q45 faced were Medium-High. Now, let’s compare it with the level of difficulty of Verbal questions that people with V45 faced (I had only two such data points with me).
Attachment:
Verbal Diff.jpg [ 22.42 KiB | Viewed 6205 times ]
Per GMAC, the guys with V45 faced mainly medium-level Verbal questions, and medium-high questions only in the second quarter.
According to you, what would be the difficulty level of the Verbal questions a person with V45 would face?
Would you call that difficulty level ‘medium’?
I believe most of us, non-native speakers, will say no. At V45 level, we’d expect very difficult questions.
However, that is our perception, not GMAC’s perception.
Thus, even if you solve a lot of these questions correctly, you deserve a V45, not V51.
I think it’s easier to understand why there is such a difference in the perceptions of the difficulty level of questions. Indians are generally good at Quant and weak in Verbal. On the other hand, Americans are quite the opposite. Thus, GMAT, a test conducted by a US-based organization, is expected to reflect the perceptions it currently reflects.
To answer the question, GMAC hasn’t deliberately made it difficult to score high on Verbal than on Quant. We feel that GMAC has done so because with Verbal, our comfort is much less than the comfort of an average test-taker in America, in which GMAC is based. The Verbal questions that are pretty hard for us are manageable for them, and the quant questions that are manageable for us are pretty hard for them.
That’s it for this article. In the next article, we’ll answer the following questions:
- Are the first few questions more important than the remaining ones?
- Does the GMAT algorithm follow a fixed pattern i.e. giving similar difficulty level of questions for similar performance?
You can find the next and last part of this article series on this link: https://gmatwithcj.com/articles/data-dri ... at-part-3/
rahul2013
Joined: 02 Jun 2013
Last visit: 21 Jul 2021
Posts: 33
Own Kudos:
Given Kudos: 142
Location: United States
Schools: IIMA PGPX'22
GMAT 1: 650 Q49 V30
Products:
10 Feb 2019, 08:10
Kudos
Bookmarks
What an article Sir...
Thank you very much
Thank you very much
