Although this is not an out and out problem on max-min, we can use the concept of max-min to rule out statements and hence answer options.
In a max-min problem on inequalities, write down the given inequalities one below the other ensuring that the inequality signs are the same in both. Then, we take 4 extreme cases to find out the maximum and the minimum values of the given expression.
Applying this principle on the given inequalities will make it clearer. Let’s start with statement I; applying the max-min principle as outline above, our calculation can look like the one shown in the image.
Attachment:
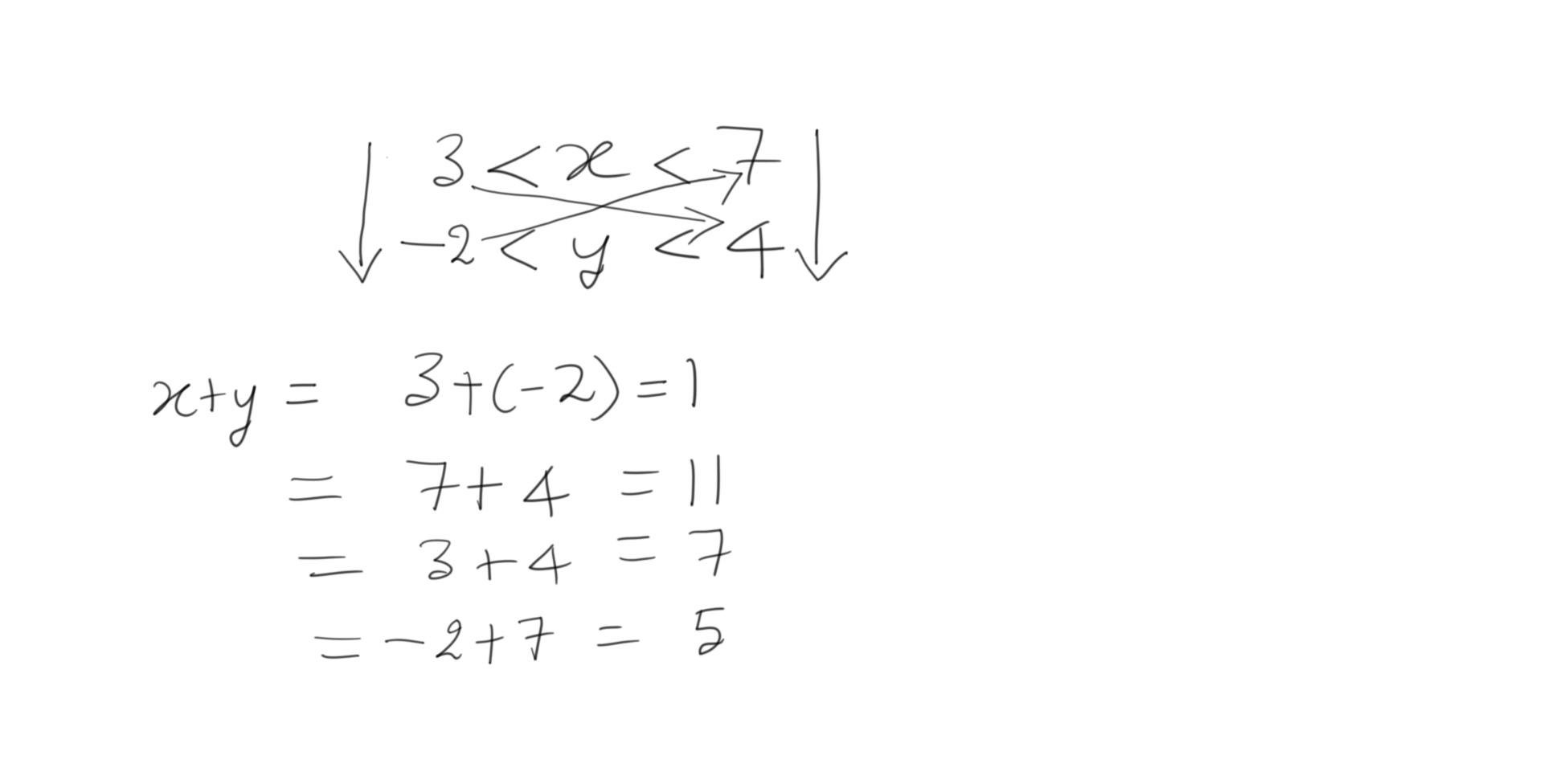 02nd July 2020 - Reply 3 - 1.jpg [ 49.27 KiB | Viewed 3356 times ]
02nd July 2020 - Reply 3 - 1.jpg [ 49.27 KiB | Viewed 3356 times ]
It’s clear that the smallest value of the expression (x+y) is 1; therefore, x+y>0 is definitely true. Statement I has to be a part of our answer, therefore answer option B can be eliminated.
When we apply the max-min principle on statement II, the calculation looks like this:
Attachment:
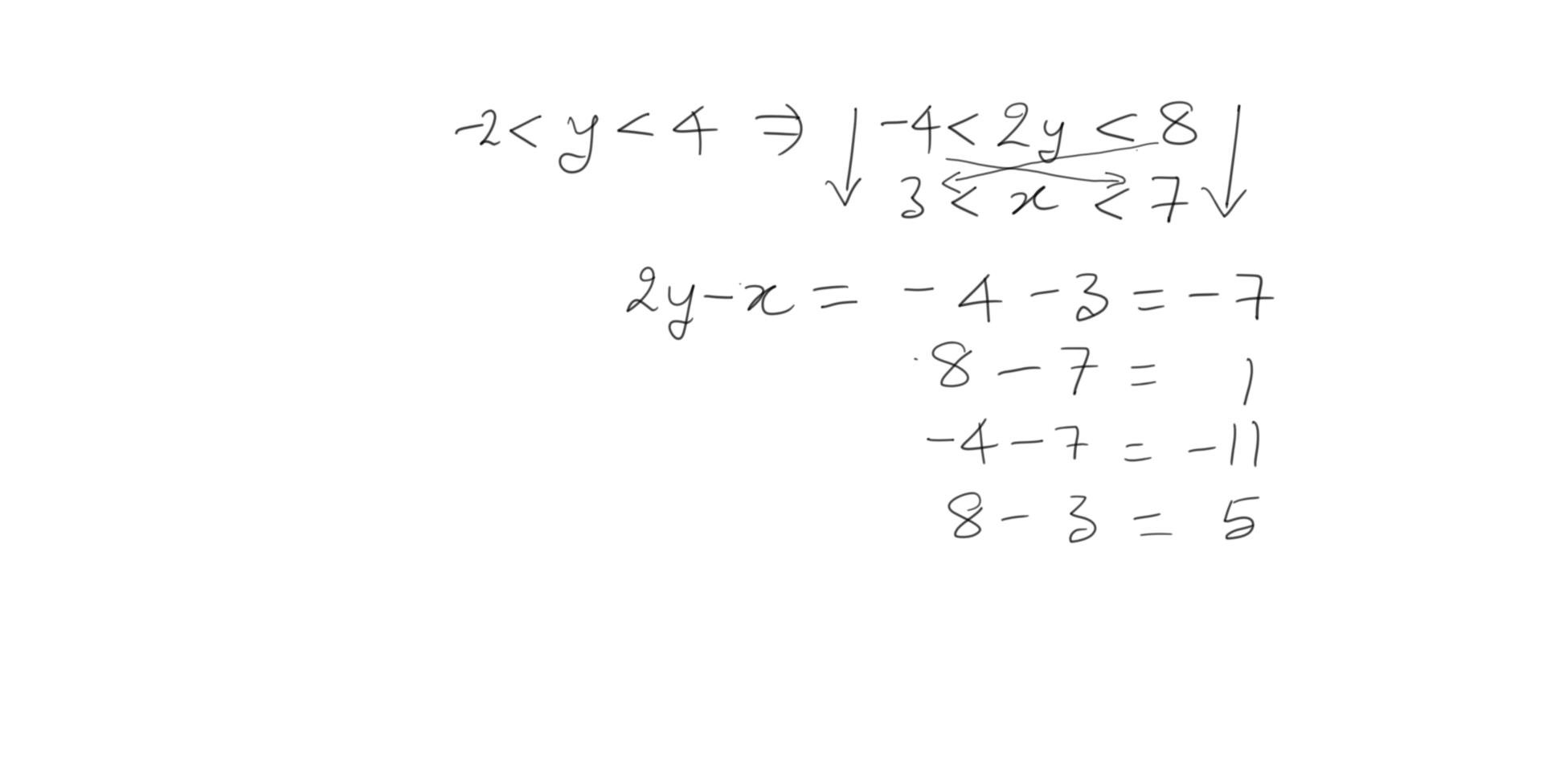 02nd July 2020 - Reply 3 - 2.jpg [ 48.68 KiB | Viewed 3322 times ]
02nd July 2020 - Reply 3 - 2.jpg [ 48.68 KiB | Viewed 3322 times ]
It’s clear that the smallest value of 2y-x is -11. Therefore, 2y-x>0 is not always true. The answer options containing statement II viz., C and E can be eliminated.
When we evaluate statement III in a similar manner,
Attachment:
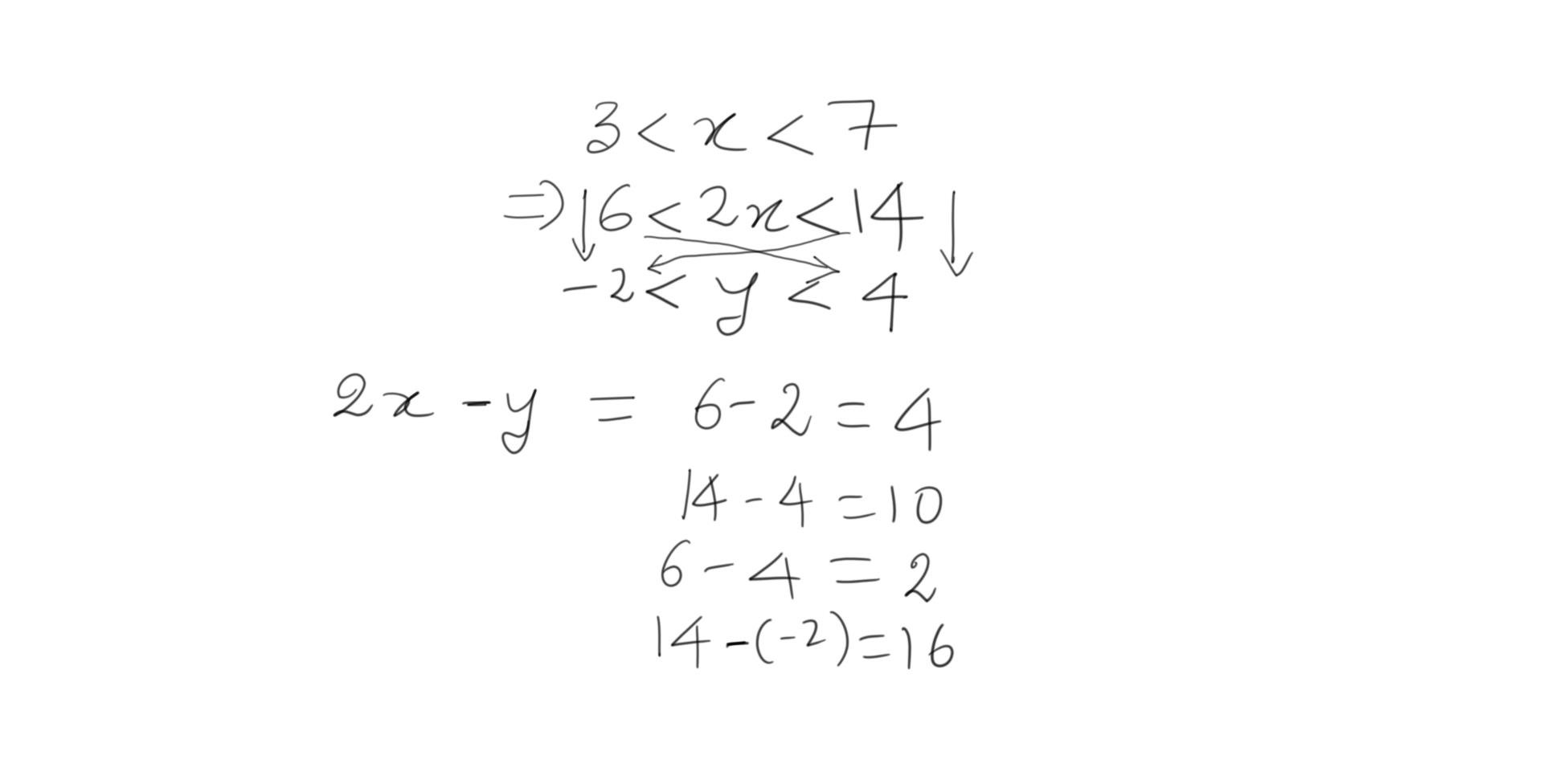 02nd July 2020 - Reply 3 - 3.jpg [ 50.52 KiB | Viewed 3337 times ]
02nd July 2020 - Reply 3 - 3.jpg [ 50.52 KiB | Viewed 3337 times ]
We find that the smallest value of the expression 2x – y is 2. Therefore, 2x – y > 1 is definitely true and hence answer option A can be eliminated. The only answer option left is D, which HAS TO be the correct answer.
The correct answer option is D.
Hope that helps!
Arvind

 15%
(low)
15%
(low)
 15%
(01:38)
wrong
15%
(01:38)
wrong  based on 107
sessions
based on 107
sessions