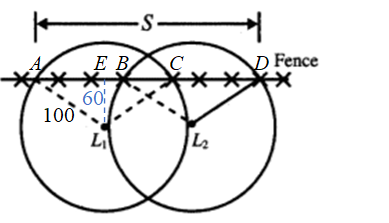
In the figure above, two security lights, L1 and L2 , are located 100

Answer: A (260).

The lights make a 90 degree angle with the fence and hence the vertical distance is 60 feet. The lights cover 100 feet of radius , which means the triangle made is a pythagorus one with 100, 60 and uknown variable (calculate it to get 80). Thus, the light L1 covers a distance of 2(80) on fence and the L2 covers a little more than 80, making a total of more than 240.

The distance from L1 to L2 is 100.
If we drop a perpendicular from L1 to the fence at P and from L2 to the fence at Q, then the distance between P & Q will be 100. (L1 L2 Q P will be a rectangle)
100 . 80 . 60 triangle is formed with the radius, fence and distance between fence & light source.
So total distance = 80+100+80 = 260

Solution:


Let’s name the 4 intersection points of the fence with the circles as A, B, C, and D (see diagram above) and notice that we need to find the length of AD. Furthermore, let’s name one more point, E, where E is the midpoint of AC. We see that AEL1 is a right triangle; in fact it’s a 3-4-5 right triangle. Therefore, AE = 80 and AC = 2 x 80 = 160. Since BD = AC,then BD = 160 also. Notice that AD = AC + BD - BC, AD = 160 + 160 - BC = 320 - BC. If we can find the length of BC, we can determine the length of AD. However, we can see that BC has a length of less than 80 since it is less than EC, which has a length of exactly 80. Since BC < 80, therefore AD = 320 - BC will be greater than 240. Since the only answer choice that is greater than 240 is 260, choice A must be the correct answer.

(Note: This means BC must be 60, but we will leave the readers to verify this on their own.)

Alternate Solution:


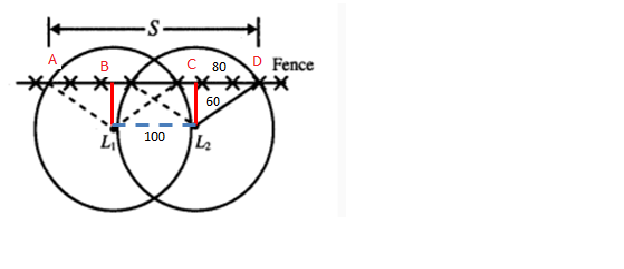
Note that the distance S is equal to the distance from A to D. We can find the length of AB, the length of CD, and then the length of BC.

First recognize triangle ABL1 as a 3-4-5 triangle, with lengths 60, 80, and 100. Thus, the length AB = 80. This is the same as the length CD because triangle DCL2 is also a 3-4-5 triangle, so CD = 80.

Note that the distance from B to C is equal to the distance from L1 to L2, and this is given as 100.

Thus, the total distance is 80 + 100 + 80 = 260.

Answer: A

It's easier if you 1st take the 2 Triangles out of the Circle and Flip them over so they are easy to look at it.

Rule - Since the 2 Triangles are Isosceles Triangles with Sides = Radius = 100, the Median from the Apex Vertex to the Non-Equal Side will Bisect that Opposite Non-Equal Side.

L1 and L2 being 60 feet away from the Fence = the Straight Line Distance dropped from the Apex Vertices (L1 and L2) and drawn Perpendicular to the Opposite NON-Equal Side = the Median that Bisects the Opp. Side in HALF = which is equal to the Height of 60

Now 2 Right Triangles are created in each of the Triangles.

1 Leg = 60 and Hypotenuse = 100

all 4 Sub Triangles are 3-4-5 Common Right Triangle. Thus, for each of the 4 Sub Triangles, the Distance Length from the Edge of the Triangle to the Median Point on the Bisected Side is = 80.

The Distance from the Median Point to the other Median Point between the 2 Triangles = Distance from the L1 Vertex to the L2 Vertex = Given as 100


80 + 80 + 100 = 260

Answer A


EDIT: the 2nd Picture above in Scott's Post. (didn't see it at first lol)

Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.