Of the students in a school, 20 percent are in the science club and 30

Agreed, a Venn diagram is easy; I drew one immediately.
Careful with the question's wording: "[W]hat percent of the students who are in the science club are not in the band?"
"S . . .but not B" means "S only" (they are only in S, and not at all in B)
This percent means \(\frac{S.Only}{S.total}*100\)

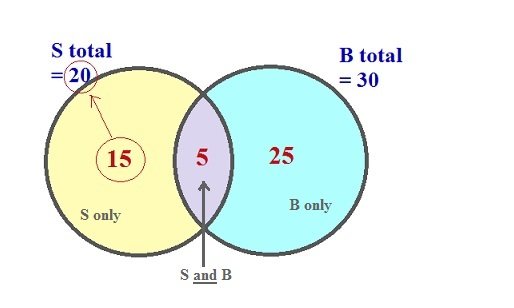
Assume 100 students. Science club = S. Band = B
S total: 20% of all students = 20
B total: 30% of all students = 30

"25 percent of the students in the school are in the band but are not in the science club"
B but not S = "B only": 25% = 25
None of those 25 students can be in the overlap,
because the overlap contains B and S.
So 25 in B only (turquoise)

Number of students in both S and B, i.e. overlap? Use B total = 30
25 of 30 are B only
The other 5 must be in the overlap (lavender). There is no other category. Thus
Overlap, the number of students who are in both: S and B = 5

Now fill in S only.
S only? = (S total - overlap)
S only: (20 - 5) = 15 (yellow)

"What percent of the students who are in the science club are not in the band?"
Percent of all S who are not B? (OR: Percent of all S who are S only? OR: "S Only" is what percent of "all S"?)
\(\frac{15}{20}=\frac{3}{4}=(.75*100)=75\) percent

Answer E