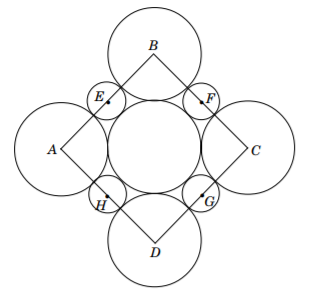
Four circles of radius 2 with centers A, B, C and D are arranged symme

All large circles have equal radii, \(r\) = 2. All small circles have equal radii.*

Find the length of the square's diagonal.
From the length of the diagonal, find the length of the side of the square**:
\(s\sqrt{2}=d\) and
\(s=\frac{d}{\sqrt{2}}\)

From the square's side, subtract the radii length of the two large circles: that is the diameter of small circle.

Divide the result by 2 to get the radius of small circle.

(1) Length of square's diagonal AC (see diagram)

The diagonal of the square runs only through large circles.
Given: \(r =2\)

Diagonal length = \((r) + (2r) + (r) = 4r\)
Diagonal length = \((2 + 4 + 2) = 8\)

(2) Calculate the side length, \(s,\) from the diagonal, \(d\)

\(s = \frac{d}{\sqrt{2}}\)

\(s = \frac{8}{\sqrt{2}} = (\frac{8}{\sqrt{2}} * \frac{\sqrt{2}}{\sqrt{2}})=4\sqrt{2}\)

(3) Find diameter of small circle from the length of the side of the square
From above, \(s = 4\sqrt{2}\)

Diameter of small circle = (side length) - 4
Because
\(s\) = (radius of circle B) + (diameter of small circle F) + (radius of circle C) (see diagram, BC)
\(s\) = (2) + (diameter of small circle) + (2)
\(s\) = (diameter of small circle) + 4
diameter of small circle = \((s - 4) = (4\sqrt{2} - 4)\)

(4) Radius of small circle is half of that diameter:

Radius of small circle = \(\frac{4\sqrt{2} - 4}{2}\)

Radius of small circle = \(2\sqrt{2} - 2\)

Answer C


*All the circles are tangent. Their common tangency points are perpendicular to their radii, thus all radii lie on the same line(s).
The radii can be summed to find diagonal and side of square.

** Derived from properties of squares/isosceles right triangles
\(s^2+s^2=d^2\)

\(2s^2 = d^2\)

\(\sqrt{2}\sqrt{s^2} = \sqrt{d^2}\)

\(\sqrt{2}s=d\)
\(s = \frac{d}{\sqrt{2}}\)