Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 19
12:30 PM EST
-01:30 PM EST
Learn how Keshav, a Chartered Accountant, scored an impressive 705 on GMAT in just 30 days with GMATWhiz's expert guidance. In this video, he shares preparation tips and strategies that worked for him, including the mock, time management, and more - Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 20
01:30 PM EST
-02:30 PM IST
Learn how Kamakshi achieved a GMAT 675 with an impressive 96th %ile in Data Insights. Discover the unique methods and exam strategies that helped her excel in DI along with other sections for a balanced and high score. - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 24
07:00 PM PST
-08:00 PM PST
Full-length FE mock with insightful analytics, weakness diagnosis, and video explanations! - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 26 Aug 2016, 02:04.
Last edited by EgmatQuantExpert on 07 Aug 2018, 02:39, edited 8 times in total.
Last edited by EgmatQuantExpert on 07 Aug 2018, 02:39, edited 8 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
Wavy Line Method Application - Complex Algebraic Inequalities
Many of you are familiar with the Wavy Line Method used to solve inequalities containing algebraic expressions in single variable. This method helps identify the range of values satisfying an inequality.
For instance, consider the following question:
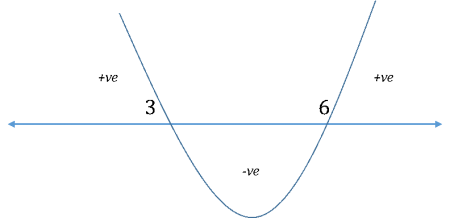
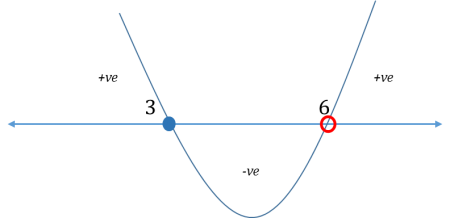
Question: Find the range of values of x satisfying the inequality \((x – 3)(x – 6) < 0\).
To solve this inequality, you draw the wavy line as follows:
And your inferences regarding the expression \((x – 3)(x – 6)\) would be:
Since the above question asks for the range of values of x for which the expression is negative, the answer would be \(3 < x < 6\).
Well, that was a simple question, so application of the wavy line method was fairly straight-forward.
Now, for many test takers, things can seem complicated as exponents and algebraic fractions are added into the mix. However, the application of this method is pretty straightforward in such scenarios too.
In this article we’ll be focusing on such complex application of the wavy line method and list out the two fundamental rules that are used to draw the wavy line to solve any inequalities testing such algebraic expressions on the GMAT.
(This article benefits those who are not familiar with the wavy line method. The rules provided in this article are generic and can be utilized for all cases. )
)
When there are multiple instances of the same root:
Try to solve the following inequality using the Wavy Line Method:
\((x−1)^2 (x−2) (x−3) (x−4)^3 < 0\)
Did you notice how this inequality differs from the example above?
Notice that two of the four terms had an integral power greater than 1.
How to draw the wavy line for such expressions?
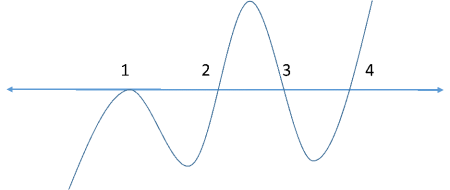
Let me directly show you how the wavy line would look and then later on the rule behind drawing it.
To know how you did, compare your wavy line with the correct one below.
Notice that the curve bounced back at the point \(x = 1\). (At every other root, including \(x = 4\) whose power was \(3\), it was simply passing through them.)
Can you figure out why the wavy line looks like this for this particular inequality?
(Hint: The wavy line for the inequality \((x−1)^{38} (x−2)^{57} (x−3)^{15} (x−4)^{27} < 0\) is also the same as above)
Come on! Give it a try.
If you got it right, you’ll see that there are essentially only two rules while drawing a wavy line.
Remember: We’ll refer the region above the number line as positive region and the region below the number line as negative region.
What do you need before drawing the wavy line?
How to draw the wavy line?
For instance, in the above example, observe the behavior of the wave at the points \(2\), \(3\), and \(4\).
However, if the power of a term is even, then the wave bounces back into the same region. Observe the behavior of the wave at the point \(x = 1\) (the term \((x-1)\) has an even power in the above expression).
Now look back at the above expression and analyze your wavy line. (Refer to the complete wavy line provided above if required)
Solution
Once you get your wavy line right, solving an inequality becomes very easy. For instance, for the above inequality, since we need to identify the range where the above expression would be less than zero, look for the area(s) in your wavy line diagram where the curve is below the number line.
So the correct solution set would simply be {\(3 < x < 4\)} \(U\) {{\(x < 2\)} – {\(1\)}}
In words, it is the Union of two regions – region1 between \(x = 3\) and \(x = 4\) and region2 which is \(x < 2\), excluding the point \(x = 1\).
Food for Thought
Now, try to answer the following questions:
What if the algebraic expression contains a fraction?
Consider the following inequality.
\(\frac{(x – 3)}{(x – 6)} ≤ 0\)
How would you apply the wavy line method to solve the above inequality?
The good news is it’s still the same process!
However, we need to keep in mind, the following things.
So our solution set becomes \(3 ≤ x < 6\)
(Once again, observe that the point \(x = 3\) is included in the solution while \(x = 6\) is excluded.)

Foot Note: Although the post is meant to deal with inequality expressions containing multiple roots, the above rules to draw the wavy line are generic and are applicable in all cases.
- Krishna
Wavy Line Method Application - Complex Algebraic Inequalities
Many of you are familiar with the Wavy Line Method used to solve inequalities containing algebraic expressions in single variable. This method helps identify the range of values satisfying an inequality.
For instance, consider the following question:
Question: Find the range of values of x satisfying the inequality \((x – 3)(x – 6) < 0\).
To solve this inequality, you draw the wavy line as follows:
And your inferences regarding the expression \((x – 3)(x – 6)\) would be:
- 1. The expression will be positive for the range of values for which the curve is above the number line.
- a. In the above example, the pertinent ranges are \(x < 3\) and \(x > 6\). So, any value of \(x\) either less than \(3\) or greater than \(6\) will make the above expression positive in sign.
- a. In the above example, the pertinent points are \(x = 3\) and \(x = 6\). So, both these values make the expression zero.
- a. In the above example, there is only one portion where the curve is below the number line and this portion corresponds to the range \(3 < x < 6\). So, any value of \(x\) strictly between \(3\) and \(6\) will make the above expression negative in sign.
Since the above question asks for the range of values of x for which the expression is negative, the answer would be \(3 < x < 6\).
Well, that was a simple question, so application of the wavy line method was fairly straight-forward.
Now, for many test takers, things can seem complicated as exponents and algebraic fractions are added into the mix. However, the application of this method is pretty straightforward in such scenarios too.
In this article we’ll be focusing on such complex application of the wavy line method and list out the two fundamental rules that are used to draw the wavy line to solve any inequalities testing such algebraic expressions on the GMAT.
(This article benefits those who are not familiar with the wavy line method. The rules provided in this article are generic and can be utilized for all cases.
When there are multiple instances of the same root:
Try to solve the following inequality using the Wavy Line Method:
\((x−1)^2 (x−2) (x−3) (x−4)^3 < 0\)
Did you notice how this inequality differs from the example above?
Notice that two of the four terms had an integral power greater than 1.
How to draw the wavy line for such expressions?
Let me directly show you how the wavy line would look and then later on the rule behind drawing it.
To know how you did, compare your wavy line with the correct one below.
Notice that the curve bounced back at the point \(x = 1\). (At every other root, including \(x = 4\) whose power was \(3\), it was simply passing through them.)
Can you figure out why the wavy line looks like this for this particular inequality?
(Hint: The wavy line for the inequality \((x−1)^{38} (x−2)^{57} (x−3)^{15} (x−4)^{27} < 0\) is also the same as above)
Come on! Give it a try.
If you got it right, you’ll see that there are essentially only two rules while drawing a wavy line.
Remember: We’ll refer the region above the number line as positive region and the region below the number line as negative region.
What do you need before drawing the wavy line?
- 1. You need to draw a horizontal line – this will be our Number Line to identify the ranges.
2. Mark the “zero points”: Note the values at which at least one of the factor terms in the expression become zero.
- a. Eg: For instance, in the above expression, the term \(x – 1 = 0\) at the point \(x = 1\), the term \(x – 2 = 0\) at the point \(x = 2\), and so on. So, we need to mark the points \(1\), \(2\), \(3\), and \(4\) on the number line.
How to draw the wavy line?
- 1. How to start: Once you draw the number line and mark the zero points on the number line, it’s time to draw the wavy line. Start from the top right most portion. Be ready to alternate (or not alternate) the region of the wave based on how many times a point is root to the given expression.
2. How to alternate:
if the power of a term is odd, then the wave simply passes through the corresponding point (root) into the other region (to –ve region if the wave is currently in the positive region and to the +ve region if the wave is currently in the negative region).
For instance, in the above example, observe the behavior of the wave at the points \(2\), \(3\), and \(4\).
However, if the power of a term is even, then the wave bounces back into the same region. Observe the behavior of the wave at the point \(x = 1\) (the term \((x-1)\) has an even power in the above expression).
Now look back at the above expression and analyze your wavy line. (Refer to the complete wavy line provided above if required)
Solution
Once you get your wavy line right, solving an inequality becomes very easy. For instance, for the above inequality, since we need to identify the range where the above expression would be less than zero, look for the area(s) in your wavy line diagram where the curve is below the number line.
So the correct solution set would simply be {\(3 < x < 4\)} \(U\) {{\(x < 2\)} – {\(1\)}}
In words, it is the Union of two regions – region1 between \(x = 3\) and \(x = 4\) and region2 which is \(x < 2\), excluding the point \(x = 1\).
Food for Thought
Now, try to answer the following questions:
- 1. Why did we exclude the point \(x = 1\) from the solution set of the last example? (Easy Question)
2. Why do the above mentioned rules (especially rule #2) work? What is/are the principle(s) working behind the curtains?
What if the algebraic expression contains a fraction?
Consider the following inequality.
\(\frac{(x – 3)}{(x – 6)} ≤ 0\)
How would you apply the wavy line method to solve the above inequality?
The good news is it’s still the same process!
- • Draw the number line
• Mark the zero points
• Draw the wavy line per the above rules
However, we need to keep in mind, the following things.
- 1. The inequality asks for “\(≤ 0\)” (less than or equal to) and not just “\(< 0\)” (less than)
- a. This is an indicator that the required range is a combination of two ranges: range of values of \(x\) for which the expression satisfies “\(<0\)’ condition and the values of \(x\) for which the expression satisfies “\(= 0\)” condition.
- a. So, we need to exclude the point \(x = 6\) from of our solution set.
So our solution set becomes \(3 ≤ x < 6\)
(Once again, observe that the point \(x = 3\) is included in the solution while \(x = 6\) is excluded.)

Foot Note: Although the post is meant to deal with inequality expressions containing multiple roots, the above rules to draw the wavy line are generic and are applicable in all cases.
- Krishna
Attachments
![]() Wavy Line Method Application - Complex Algebraic Inequalities.pdf [604.57 KiB]
Wavy Line Method Application - Complex Algebraic Inequalities.pdf [604.57 KiB]
Downloaded 1682 times
Originally posted by EgmatQuantExpert on 26 Aug 2016, 02:35.
Last edited by EgmatQuantExpert on 07 Aug 2018, 02:50, edited 4 times in total.
Last edited by EgmatQuantExpert on 07 Aug 2018, 02:50, edited 4 times in total.
Kudos
Bookmarks
Exercise Questions
Here is a list of questions specifically designed to help you apply the learnings from this article.
Question 1
Question 2
Question 3
Question 4
Question 5
Question 6
Question 7
Detailed solutions will be posted soon.
Happy Learning!
Here is a list of questions specifically designed to help you apply the learnings from this article.
Question 1
Question 2
Question 3
Question 4
Question 5
Question 6
Question 7
Detailed solutions will be posted soon.
Happy Learning!
General Discussion
Kudos
Bookmarks
Hello,
I found this process of yours extremely helpful and intuitive. Thanks!
A point has been bothering me a lot and I have not been able to answer it myself:
When drawing the wavy line, why do we always start from the top right corner rather than the bottom right corner? Maybe this is a dumb question and the answer is obvious, but I can't figure it out.
Can a curve never end sloping downwards?
Thanks!
I found this process of yours extremely helpful and intuitive. Thanks!
A point has been bothering me a lot and I have not been able to answer it myself:
When drawing the wavy line, why do we always start from the top right corner rather than the bottom right corner? Maybe this is a dumb question and the answer is obvious, but I can't figure it out.
Can a curve never end sloping downwards?
Thanks!