On the x y plane, there are 8 points of which 4 are collinea

My answer is A 28.(quite skeptical).

Let the 4 collinear points be A,B,C,D. then I can join AB as 1 line, BC as 1 line,CD as 1 line. AC as 1 line. AD as 1, BC,CD as 2 more.
Giving a total of 6 lines.--(1)
My reasoning here is question says the number of line that CAN be formed by joining any 2 points.
So all the above lines can be treated as different lines between 2 points. Like line AD passes through points B and C but in essence it is a different line to BC or CD.

Next each non collinear point will have 1 passing through A,B,C and D..hence all 4 non collinear pints will in total have 16 lines.--(2)

And between the 4 non collinear we can for 6 lines.(4C2) or you can visualise these 4 points to be the corners of a square so you will have 4 sides and 2 diagonals. total 6 lines.--(3)

hence total number of lines are (1)+(2)+(3) = 6+16+6=28.

Umm mdbharadwaj don't you think the 6 line-segments joining the collinear points can actually considered to be one unique line. If we are not considering unique lines, then the number is bound to increase significantly.

Regards,
Arpan

I thought of that, however the questions asks for the number of line segments that can be formed between any 2 points.
Consider numbers 1,2,3,4 on the number line.
So line 1-2 is different from line 3-4. 1-2 is an unique line between points 1 and 2 so is 3-4. And the number doesn't increase significantly , as there will be a maximum of 28 lines.
Because if we consider the line joining the 4 collinear points to be 1 single line or to be 6 different lines, the number of lines between the the non collinear points themselves and the collinear points will not change. there will be 16+6 = 22 lines only.

Hope I got my point across.

Lemme just clarify my idea over this. Please refer to my *supremely sloppy* paint-work attached (Apologize for that ). You can see, that A, B and C lie on the line L. Now As the question states:


Now, If I am to consider a straight line passing through A and B, it would be L. Again if I am to consider a straight line passing through B and C, it would be L. Same is the case for A and C as well. The A-B, B-C and C-A are segments. L is the only unique straight line passing through the collinear points. Getting back to the question, you are spot-on for the 16 and 6 values. After adding the one line that passes through the collinear points, I believe you have the answer! Hope I am correct! Mods please verify!

Regards,
Arpan

**edited for a typo! sorry!

Number of ways two points can be selected from the 8 points is 8C2.
Number of lines that can be formed by the collinear points if they were non collinear is 4C2.
Therefore total number of lines is 8C2 - 4C2 + 1(one for the line which is formed by the collinear points)

Dear Responders,

Thank you all for participating in this quiz, coming with your detailed solutions, and having a thoughtful debate here. I would also like to congratulate all interns as well for being the part of this glorious community.

At first I would like to inform you that this question and its logic is based on the question given in Indian school text book (CBSE / Class XI / Volume II / Chapter 35 - Combinations / Page 35.13 / Author - Shri R. D. Sharma). The snapshot of this reference question is also given herewith for your clear understanding.

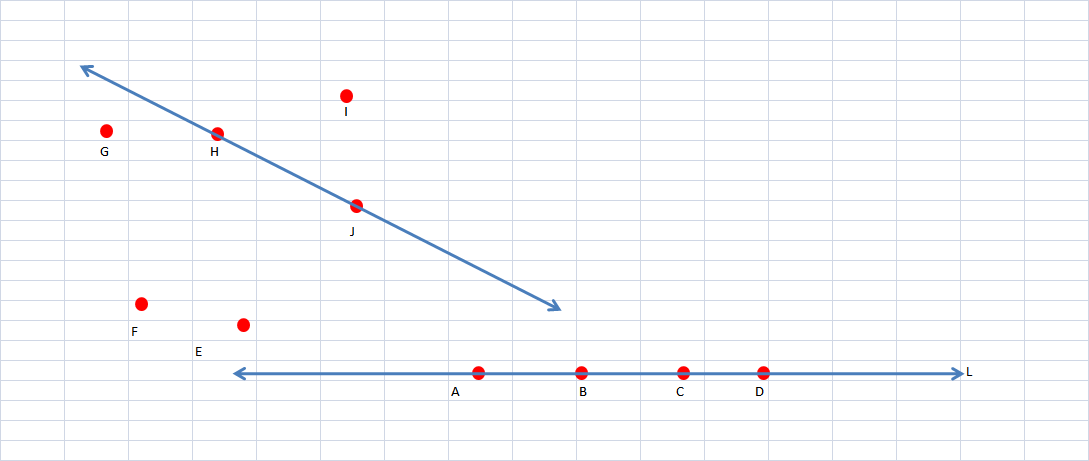
We have 8 points on x y plane of which 4 are collinear. We should know that the 4 collinear points can not form any other line among them except for 1 that will connect two extremes. (We are discussing here about a line and not about a line segment)

Connecting any two points from 8 points is similar to choose 2 things from 8. This can be done in 8C2 ways.
Note these 8C2 combinations also include the combination of fictitious lines that can be formed from 4 collinear points. This we can calculate as 4C2
We also have to include 1 line (formed by connection collinear extremes) in above combinations.

Hence Total Number of Combinations will be 8C2 - 4C2 + 1 ------> 28 - 6 + 1 = 23 = Choice D.

This logic we can take further in triangle case
Number of triangles = 8C3 - 4C3 (Here collinear extremes will not form any triangle, so no need to add 1 in this case)


Question indeed asks for number of lines and not for number of line segments.

Those who gave correct solution have been awarded Kudos. In exceptional case, Kudos has also been awarded to 'mdbharadwaj' for his honest fight and to encourage him/her for further contribution.

Thank You,

Regards,

Narenn

8 points total - 4 are collinear (lie along a straight line) and 4 are non-collinear.

a) All the collinear points lie on a straight line - 1 line can be drawn through them.
b) Use combinations for the remaining 4 non-collinear points. We use combinations because, the order of the points along a line do not matter. We have 4 total points to choose from, and we can choose only 2 points to draw a line through. Hence, it is 4C2. 4C2 = 4!/(2!*2!) = 6. Thus, 6 lines can be drawn here.
c) Each non-collinear point can draw a unique line through each collinear point. That is, 4 non-collinear points * 4 collinear points = 16 possible lines.

Thus there are 1+6+16=23 possible lines that can be drawn.
The correct answer should be D.

Thank you for the question, Narenn.

Similar questions to practice:
the-sides-bc-ca-ab-of-triangle-abc-have-3-4-5-interior-109690.html
abcde-is-a-regular-pentagon-with-f-at-its-center-how-many-133328.html
m03-71107.html
if-4-points-are-indicated-on-a-line-and-5-points-are-132677.html

Hope it helps.

Hi All,

Another way to think about this set-up is to 'map out' the options (without physically drawing them all).

I'm going to call the first 4 points A, B, C, and D and the 4 collinear points E, F, G, and H

Point A can form a line with any of the other 7 points = 7 lines
Point B can also form a line with any point (but already formed a line with point A, so we can't count that line twice) = 6 lines
Point C already formed lines with Point A and Point B.....= 5 lines
Point D = 4 lines

+ 1 more line formed by EFGH....

7+6+5+4+1 = 23 lines

Final Answer:

GMAT assassins aren't born, they're made,
Rich

Another way would be the following:
total number of formations is 8C2=28
number of lines that can be formed by 4 points is 4C2=6 (so 1 line has 5 duplicates) thus total is 28-5=23

Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.